Cheat sheet - Haj Ali
Author @hajali-amine
SLD Resolution
Logic programming is based on a specific resolution strategy called SLD resolution (Selective Linear Definite resolution).
- Based on linear resolution.
- Generally, this method is incomplete.
- It is complete when applied to definite clauses.
- a is a definite clause, also referred to as an atomic clause. (a being an atom).
- a<=b is a definite clause, also referred to as a rule, where a, the head, is an atom and b is a body.
- A knowledge base is a set of definite clauses.
Prolog
Prolog is intended primarily as a declarative programming language; the program logic is expressed in terms of relations, represented as facts and rules. A computation is initiated by running a query over these relations.
Important note:
When we write a goal like X = Y in Prolog, we are testing for more than simple equality in the mathematical sense. We are testing whether X (which might be a variable, an atom, or an arbitrarily complex term) unifies with Y (which might also be an atom, a variable, or a term). Whenever you write "=" in a Prolog procedure, review the code to see whether you can get rid of the "=" clause by replacing the item on the left of "=" by the item to the right of it, elsewhere in the procedure.
Example
- Socrates is a human.
- All humans are mortal.
- Is Socrates mortal?
In prolog, this will be translated to;
human(socrates).
% X is a variable
mortal(X):-human(X).
mortal(socrates).
Execution
| IMPORTANT |
|---|
| Prolog explores the rules in the order of their implementation in the program, it explores the list of goals from the left to the right, and creates a search tree. |
Execution of a Prolog program is initiated when the user writes a query. Logically, the Prolog engine tries to find a resolution refutation of the negated query. If the negated query can be refuted, it follows that the query, with the appropriate variable bindings in place, is a logical consequence of the program. In that case, all generated variable bindings are reported to the user, and the query is said to have succeeded.
Operationally, Prolog's execution strategy can be thought of as a generalization of function calls in other languages, one difference being that multiple clause heads can match a given call. In that case, the system creates a choice-point, unifies the goal with the clause head of the first alternative, and continues with the goals of that first alternative. If any goal fails in the course of executing the program, all variable bindings that were made since the most recent choice-point was created are undone, and execution continues with the next alternative of that choice-point. This execution strategy is called chronological backtracking.
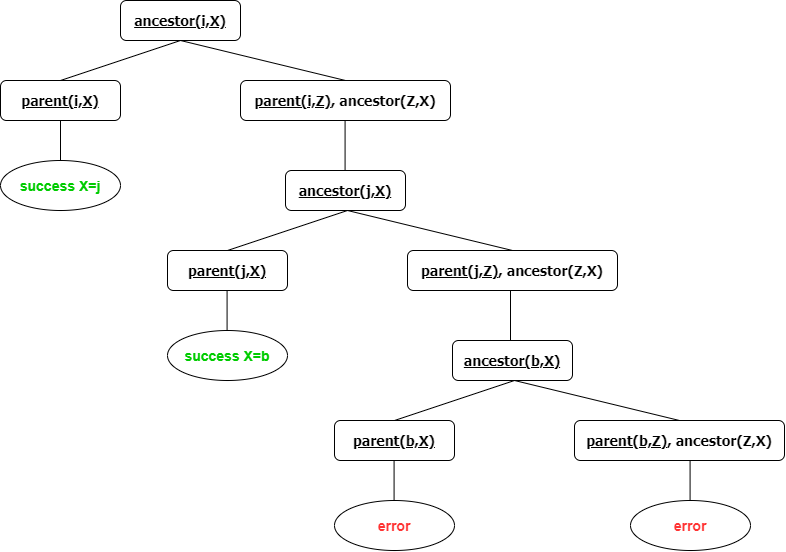
Execution Example
parent(i,j).
parent(j,b).
ancestor(X,Y):-parent(X,Y).
ancestor(X,Y):-parent(X,Z),ancestor(Z,Y).
ancestor(i,X).
Execution:
Arithmetics
Prolog knows integers and floats.
An arithmetic expression is created using numbers, variables and arithmetic operators.
Usual operators:
| Operator | Description |
|---|---|
+ | Addition |
- | Substraction |
* | Multiplication |
// | Integer division |
/ | Float division |
mod | Rest of division |
Predefined mathematical functions:
| Function | Description |
|---|---|
abs(X) | Absolute value |
log(X) | The log function |
sqrt(X) | Square root |
exp(X) | The exponential function |
sign(X) | The sign function |
random(X) | Evaluates to a random integer i, 0<=i<X |
sin(X) | The sine function |
cos(X) | The cosine function |
tan(X) | The tangent function |
max(X,Y) | The maximum function |
min(X,Y) | The minimum function |
Be careful! Expressions are represented with trees in prolog!
X = 3 + 2.
% X=3+2
X + Y = 3 + 2.
% X=3, Y=2
This is easily explained by the fact that expressions are represented with trees and the = operator is used for the unification.
Exp1 =:= Exp2, is successful if the two expressions are equal. (The opposite of the the=\=operator)Exp1 < Exp2, is successful if the value of Exp1 is strictly inferior than Exp2. (The opposite of the the>operator)Exp1 =< Exp2, is successful if the value of Exp1 is inferior or equals Exp2. (The opposite of the the>=operator)
Unification
| Comparaison | Unification |
|---|---|
X == Y, is successful if X is identical to Y whereas X \== Y, is successful if X is not identical to Y. | X = Y, unifies X with Y whereas X \= Y, is successful if X is not unifiable with Y. |
X is 9 mod 4.
% X=1
X = 9 mod 4.
% X=9mod4
X == 9 mod 4.
%error
Recursivity
Let's take the Facrotial function as an example;
0! = 1
n! = n(n-1)! for n>0
fact(0,1).
fact(N,R):-N>0,N1 is N-1,fact(N1,R1),R is N*R1.
Dynamic manipulation
In Prolog, it is possible to modify dynamically your program by adding and removing clauses.
Predefined predicates:
| Predicate | Description |
|---|---|
asserta | adds a fact or a rule at the top of the list of facts or rules. |
assert and assertz | adds a fact or a rule at the end of the list of facts or rules. |
retract | Removes a fact or a rule from the knowledge base. |
To be able to use the predicates, you have to declare the concerned predicates using dynamic!
dynamic man/1.
% Let's add Jean is a man to our knowledge base
assert(man(jean)).
% Now let's remove it
retract(man(jean)).
We can also write our programs in a text file, and then load them dynamically with the predicate consult/1.
% loads the file load or load.pl
consult('load').
We have other predicates, such as:
listing: lists all of the facts and the rules in our knowledge base.fail: a predicate that always gives an error.- Predicates to verify the type:
var,nonvar,integer,float,number,atom,string,... readandwrite: IO.- and so many other predicates!
Lists
A list is a data structure in Prolog which consists of a sequence of objects that can have different types.
[a, [1,2,3],X,Y] is a list.
- Empty list
[] - A list that are not empty
[a,b,c] - Lists' constructor
|[Head | Rest][a]is the same as[a | []][a,b]is the same as[a | [b]]which is the same as[a | [b | []]]
[a,b,c]=[X|L].
%X=a, L=[b,c]
[1|L]=[1,2,3].
%L=[2,3]
[1,2,3|L]=[1,2,3].
%L=[]
[a,b|L]=[1,2,3].
%error
[a,b|L]=[a,b,3,4].
%L=[3,4]
[Y]=[].
%error
[X, Y] = [1| [2]].
%X=1, Y=2
[X| L] = [1, []].
%X=1, L= [[]]
Predicates:
member/2
member(X, [X|_]).
member(X, [_|L]):-member(X,L).
- Mode(input, input), it verifies if an element is a member of the list.
- Mode(output, input), it lists the elements of the list.
length/2
length([],0).
length([_|L],N):-length(L,M),N is M+1.
- Mode(input, input), it verifies if the length of the list given in input is right.
- Mode(input, output), it returns the length of the list.
append/3
append([],L2,L2).
append([X|L],L2,[X|L3]):-append(L,L2,L3).
% thus
member(X,L):-append(_,[X|_],L).
reverse/2
reverse([],[]).
reverse([X|Xs],Ys):-reverse(Xs,Zs),append(Zs,[X],Ys).
% or
reverse([],L,L).
reverse([X|Xs],Ys,L):-reverse(Xs,[X|Ys],L).
reverse(Xs,Ys):-reverse(Xs,[],Ys).
delete/3
delete([],_,[]).
delete([X|Ys],X,Ys).
delete([Y|Ys],X,[Y|Zs]):-X =\= Y,delete(Ys,X,Zs).
permute/2
permute([],[]).
permute([X|Xs],Ys):-permute(Xs,Zs),insert(X,Zs,Ys).
insert(X,Ys,[X|Ys]).
insert(X,[Y|Ys],[Y|Zs]) :-insert(X,Ys,Zs).
findall/3, this predicate allows you to return a list of all of the objects that verifies a certain condition. Returns an empty list if condition not satisfied.
num(0).
num(1).
num(2).
num(3).
num(4).
num(5).
num(6).
num(7).
num(8).
num(9).
solution(X):-num(X),0<X*X-10*X+20.
findall(X,solution(X),L).
%L=[0,1,2,8,9]
bagof/3, same as findall except it return an error when the condition is not satisfied and the fact that it gives a list for each value of the goal's free variables.
num(0,pair).
num(1,impair).
num(2,pair).
num(3,impair).
num(4,pair).
num(5,impair).
num(6,pair).
num(7,impair).
num(8,pair).
num(9,impair).
solution(X,Y):-num(X,Y),0<X*X-10*X+20.
bagof(X,solution(X,Y),L).
%Y=impair, L=[1,9]
%Y=pair, L=[0,2,8]
Cut
- Cut or
!is a predefined predicate that is always satisfiable. - It's made to control the search tree to get rid of useless explorations.
- Cut is not logical.
H:-B1,B2,...,Bi,!,Bi+1,...,Bm.
- Once the predicate
!is executed, the choice-points in H, B1,...,Bi are deleted. - However, it can still explore other choice-points in Bi+1,...,Bm.
Why use cut?
- To stop useless explorations.
member(X,[X|Y_]):-!.
member(X,[_|Xs]):-member(X,Xs).
- If else statements.
f(X,0):-X < 3,!.
f(X,2):-X < 6,!.
f(X,4).
- Expression of the negation in Prolog.
different(X,Y):-X = Y,!,fail.
different(X,Y).
Green cut: the declarative semantic of the program isn't modified. (We can remove the cut, and the program will function.)
min(X,Y,X):- X=<Y,!.
min(X,Y,Y):- Y<X,!.
Red cut: the declarative semantic of the program is modified. (Removing the cut will lead to the malfunctioning of the program.)
min(X,Y,X):- X=<Y,!.
min(X,Y,Y).
Negation
The not in Prolog has two limitations:
- It has to be in the body of a clause.
strong(X):-athletic(X),not(small(X)).
- The
notis different from the logical negation.
r(a).
q(b).
p(X):-not(r(X)).
q(X),p(X).
% true.
p(X),q(X).
% false.
not(X) does not mean that X is always false, it means that we don't have enough information to prove X.
Each time we use the not/1, we have to create another search tree;
- if it shows a success, then the not will return false.
- if it returns all errors, the the not will return a true.
Binary search trees
The following tree can be implemented as;
t(6,t(4,t(2,nil,nil),t(5,nil,nil)),t(9,t(nil,nil,10),nil)).
member_tree/2
member_tree(X,t(_,X,_)).
member_tree(X,t(G, Root,_)):-X<Root,member_tree(X,G).
member_tree(X,t(_,_,D)):-X>Root,member_tree(X,D).
insert_tree/3
insert_tree(A,X,A1).
insert_tree(nil,X,t(nil,X,nil)).
insert_tree((t(G,X,D),X,t(G,X,D)).
insert_tree(t(G,R,D),X,t(Ag,R,D)):-X<R,insert_tree(G,X,Ag).
insert_tree(t(G,R,D),X,t(G,R,Ad)):-X>R,insert_tree(D,X,Ad).