Heap & Priority queues
Author @hajali-amine
Priority queues
Let E be a set mapped by a priority function p. We call a priority queue a data type that allows us to:
- represent E,
- add an element, with a given priority, to E,
- remove an element with the lowest/highest priority.
Implementations
| Structure | Search max/min | Insertion | Deletion |
|---|---|---|---|
| Unsorted Array | O(n) | O(1) | O(n) |
| Unsorted List | O(n) | O(1) | O(n) |
| Sorted Array | O(1) | O(n) | O(1) |
| Sorted List | O(1) | O(n) | O(1) |
Optimised implementation
| Structure | Search max/min | Insertion | Deletion |
|---|---|---|---|
| Heap | O(1) | O(log(n)) | O(log(n)) |
Heap
Level of a node
The level of a node X in a tree A is the number of edges on the path from the root node to X.
The level of the green node is 3.
Hierarchical numbering
For a binary tree A, hierarchical numbering consists of numbering, starting from 1, the nodes from top to bottom and for each level from the left to the right.

Complete binary tree
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
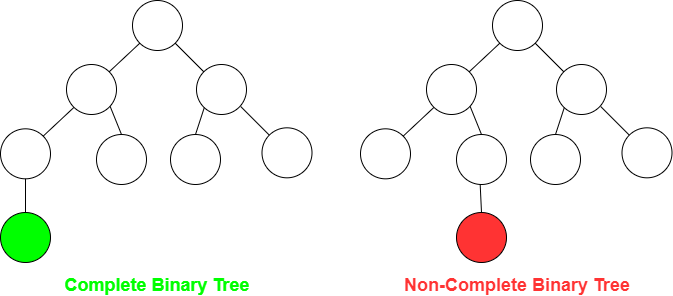
Heap : Complete binary tree
Let E be a set mapped by a priority function p. A heap representing (E,p) is a couple T=(A,obj) where A is a complete tree and obj is a bijection that maps for each node an element of E.
Thus, for all node x of A other than the root, p(obj(x))>p(obj(Parent(x)))
Structure
typedef struct{
element e;
int priority
} node;
typedef struct{
int size;
node* t;
} heap;
You may be wondering as to why we represent it as an array! Well let me explain.
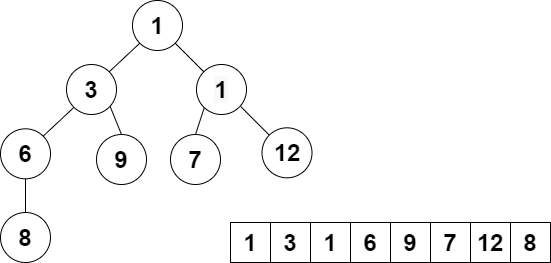
The root is the node of index 0. And for a node of index i, the parent is the node of index i-1 div 2, the left child is the node of index 2i+1 and the right child is the node of index 2i+2.
Creation
heap create(int size) {
node* t = (node*) malloc(size * sizeof(node));
heap h;
h.t = t;
h.size = 0;
return h;
}
Insertion
- Insert the element at the end of the table.
- Keep swapping withe the parent until the priority constraint is respected.
heap insert(node o, heap h) {
h.t[h.size] = o;
h.size++;
int current = h.size - 1;
int parent = (current - 1) / 2;
while (current > 0) {
if (h.t[current].priority < h.t[parent].priority) {
node temp = h.t[current];
h.t[current] = h.t[parent];
h.t[parent] = temp;
current = parent;
parent = (current - 1) / 2;
}
else
{
break;
}
}
return h;
}
Deletion
In a min heap, we can only remove the node with lowest priority! In that case, it is the root node.
- Assign the value of the last node to the root.
- Delete the last node.
- Swap with the child node with lowest priority until the priority constraint is respected.
heap delete (heap h, node* o) {
*o = h.t[0];
h.t[0] = h.t[h.size - 1];
h.size--;
int current = 0;
while (current < h.size)
{
int childMin = h.t[current * 2 + 1].priority > h.t[current * 2 + 2].priority ? current * 2 + 2 : current * 2 + 1;
if (h.t[current].priority > heap.t[childMin].priority) {
node temp = h.t[current];
h.t[current] = h.t[childMin];
h.t[childMin] = temp;
current = childMin;
}
else {
break;
}
}
return h;
}